Teoria dell'informazione
- Testo
- Bibliografia15
- Links3
- Voci correlate
Autore: Franco Lever
Va sotto il nome di t.d.i. un complesso di studi di tipo matematico che hanno come oggetto specifico della loro ricerca la trasmissione di segnali, con l’obiettivo di ottimizzarne il processo, garantendo cioè il massimo di dati trasmessi, al minimo costo, alla più alta velocità consentita dal canale, con il pieno controllo degli errori anche in presenza di disturbi non eliminabili. Alla t.d.i. è indissolubilmente legato il nome dello scienziato statunitense Claude E. Shannon.
a) affidare il messaggio a un messaggero, il quale lo recapita spostandosi fisicamente dopo averlo imparato a memoria o portandolo con sé su un qualche supporto in forma ‘scritta’ (criptato o meno);
b) utilizzare dei segnali capaci essi stessi – nonostante la distanza – di stabilire il contatto con il destinatario. È il caso dei segnali sonori (ad esempio il tam-tam, il corno, le campane...), dei segnali luminosi (il fuoco o fiaccole nella notte, i riflessi dei raggi del sole di giorno) oppure visibili da lontano (come le bandiere o il fumo...). In questo secondo caso l’uomo migliora il suo dominio sullo spazio e contrae il tempo che impiega a colmarlo, dal momento che può fare in qualche istante azioni che esigerebbero giornate, o anche mesi o anni.
La storia della comunicazione fornisce una documentazione interessante su come l’uomo abbia saputo migliorare le sue prestazioni in ambedue le direzioni, sollecitato senza tregua da una società che, crescendo e divenendo sempre più articolata, esigeva una rapidità sempre maggiore nei contatti. Più complessa infatti è l’organizzazione sociale e più vitale diviene l’interdipendenza tra attività spazialmente lontane; più alto diventa il tasso di informazione che bisogna trasmettere, più veloce deve essere lo scambio.
Seguendo il primo metodo, si è puntato a rendere sempre più veloce il messaggero (strade sempre migliori, il cavallo, il veliero, la macchina a vapore, poi i motori a combustione interna, l’aereo, i razzi...), più leggero, economico e ‘capiente’ il supporto usato (dalla pietra all’argilla, al papiro, alla pergamena, alla carta, al supporto magnetico e ottico) e più efficiente il tipo di ‘trascrizione’ (dagli ideogrammi alla scrittura sillabica, all’alfabeto fonetico completo, al linguaggio digitale...).
Nel secondo caso – quello che in questa voce ci interessa – i miglioramenti hanno puntato su un uso più efficiente del ‘contatto a distanza’ consentito dalla vista e dall’udito, giungendo a elaborare dei sistemi di segni in grado di trasmettere messaggi complessi. L’attenzione a questo secondo settore di ricerca non è nuovo. Ad esempio, lo storico greco Polibio (200-120 a. C.) nelle Storie racconta dell’invenzione di Cleonesso e di Democrito (da lui stesso ulteriormente perfezionata): con due gruppi di operatori (cinque e cinque) e dieci fiaccole, di notte o all’imbrunire, si poteva trasmettere qualsiasi messaggio. Analizzando quanto dice lo scrittore si nota che il metodo consisteva nella messa a punto di un codice secondo il quale le fiaccole – esposte o schermate e collocate in posizioni diverse – riuscivano a indicare tutte le lettere dell’alfabeto. Nonostante la sua ingegnosità, il metodo non si diffuse e finì per essere dimenticato.
Anche nel caso del telegrafo ‘ottico’ di Claude Chappe (1763-1805) – impiegato per pochi decenni, soprattutto in Francia, a partire dal 1793 – l’elemento innovativo non stava tanto nei marchingegni adottati (al posto delle fiaccole, ora, delle pale che richiamano quelle di un mulino a vento, pur se snodate e manovrabili), quanto nell’elaborazione di un codice che consente di usare in modo efficiente dei segnali riconoscibili da lontano, purché le condizioni di luce lo permettessero. Sia l’operatore che manovrava le pale sulla prima torre sia quello che sulla torre successiva interpretava le varie posizioni erano già in possesso delle tavole di corrispondenze: una certa posizione corrispondeva a una lettera dell’alfabeto, oppure – con netto miglioramento della velocità del sistema – a un intero testo già previsto dal sistema stesso, per ‘trasmettere’ il quale si indicava soltanto la corrispondente pagina del manuale di istruzioni. Non devono sfuggire la validità e il limite di questa seconda scelta: usando il telegrafo per trasmettere lettere dell’alfabeto si può trasmettere qualsiasi messaggio, ma con grande lentezza; se invece si definiscono in partenza i messaggi utili e un manuale elenca e numera i ‘pacchetti-messaggio’, si può usare il telegrafo in modo più efficiente trasmettendo soltanto i dati che individuano il ‘pacchetto’ (il numero progressivo che lo contraddistingue).
Chappe, dunque, migliora la velocità di trasmissione e la precisione (assenza di errori) del suo telegrafo ‘chiudendo’ il sistema, definendo cioè in anticipo che cosa si trasmetterà: emittente e ricevente conoscono i messaggi possibili (hanno a disposizione il prontuario), ciò che viene trasmesso è soltanto l’indicazione per individuare – tra quelli previsti – il messaggio inteso.
Le torri di Chappe – con le due grandi braccia snodate – scompaiono già nei primi decenni dell’Ottocento, non così le sue intuizioni a riguardo dell’organizzazione delle informazioni da trasmettere. Verranno riprese e approfondite ulteriormente.
La situazione cambia totalmente quando la scienza rende utilizzabili nuove forme di ‘contatto a distanza’, come l’elettricità prima e poi l’elettromagnetismo, con l’intero spettro delle onde elettromagnetiche. Si tratta di forme di energia che si muovono a velocità fantastica (nell’ordine dei 300.000 km/s) e che, pur non essendo direttamente percepibili da parte dell’uomo, diventano utilizzabili grazie alla progressiva disponibilità di strumenti che funzionano da interfaccia: il telegrafo, il telefono, la radio, la televisione, i ponti radio di ogni tipo.
Anche con questi nuovi strumenti la sfida decisiva si è giocata nella ricerca di come organizzare messaggi e segnali per ottenere la più alta efficienza. Si dice che Samuel Morse (1791-1872) – di professione pittore – abbia inventato il telegrafo e, così dicendo, si pensa al ticchettio di una manopola/interruttore manovrata da un telegrafista, a cui corrisponde, lontano a piacere, il ticchettio di un relais che appoggia una penna su una striscia di carta che scorre, in modo da tracciarvi dei punti e delle linee. Tutto questo è vero, ma il ‘nuovo’ dell’invenzione di Morse non sta in questi strumenti che egli aveva visto funzionare nelle mani di altri e che ad altri chiese di migliorare: le idee più innovative vanno riconosciute nel modo in cui egli organizzò il suo codice, in funzione di determinate caratteristiche dei messaggi da trasmettere e del canale a disposizione. Geniali e anticipatrici infatti sono alcune scelte da lui operate.
a) Suo obiettivo era trasmettere dei testi scritti. Comincia dunque con lo studio dell’alfabeto, a cui impone un ordine diverso dal tradizionale A-Z: ordina le lettere secondo il criterio della frequenza con cui esse compaiono nei testi inglesi. Non arriva ancora a servirsi di calcoli statistici per definire la probabilità di ciascuna lettera come farà C. Shannon, ma l’intuizione è già presente. Probabilmente aveva familiarità con il lavoro del tipografo, i cui cassetti non erano egualmente pieni di lettere: le ‘e’ o le ‘c’ erano molto più numerose che non lettere ‘f’ o ‘q’.
b) Sceglie i segnali da trasmettere via cavo, seguendo il criterio della sicurezza da errori: due soli segnali (chiusura del circuito per un tempo breve o per un tempo lungo), non facilmente modificabili da disturbi, tradotti all’altro capo della linea da un elettromagnete in punti (tratti brevi) e linee (tratti lunghi), tracciati su una striscia di carta in movimento, segni chiaramente riconoscibili dall’operatore.
c) Completa il codice associando le stringhe (le sequenze di punti e linee) più brevi alle lettere più frequenti: alla lettera ‘e’ associa un punto; alla ‘a’ un punto e una linea; alla ‘i’ due punti (il criterio usato è evidente, anche se non è seguito in modo perfetto; come si è detto, è utilizzato sulla base di una intuizione, non di calcoli statistici).
d) Dopo aver notato che i cavi sotterranei erano (allora) ‘inspiegabilmente’ disturbati da correnti estranee, capaci di introdurre errori non controllabili, adotta come canale le linee aeree.
Anche nel telegrafo di Morse, dunque, le vere novità non sono legate alla tecnologia utilizzata, ma al modo con cui viene trattata l’informazione: il sistema opera grazie a un codice efficiente, col quale viene sfruttata la maggiore o minore frequenza dei ‘messaggi’ da trasmettere (le lettere dell’alfabeto), utilizzando dei segnali scelti in funzione delle caratteristiche del canale per aver un miglior controllo dei possibili errori. La prova più evidente che questo è vero si ha constatando che la macchina ‘telegrafo’ ha continuato a subire modifiche e miglioramenti dall’anno della registrazione del brevetto (1837), mentre il codice Morse è rimasto ininterrottamente in uso, senza variazioni significative. (Al riguardo è interessante notare che il sistema internazionale per le chiamate di soccorso in mare ha continuato a utilizzare il codice Morse – sul canale di emergenza di 500 kHz – fino al 1° febbraio 1999, quando si è incominciato a utilizzare in forma esclusiva il GMDSS (Global Maritime Distress and Safety System), già attivo dal 1° agosto 1993. Oggi il codice Morse ha soltanto un’utilizzazione amatoriale).
Verso la fine del secolo XIX si scopre e subito si adotta un nuovo canale di comunicazione, le onde elettromagnetiche. Queste si propagano ovunque, al di là di ogni ostacolo e senza bisogno di particolari supporti. Per la loro immediata utilizzazione (Marconi) e poi per molti anni ancora si ricorre al codice Morse. Mano a mano però che si conoscono meglio i fenomeni elettrici ed elettromagnetici, vari tecnici e scienziati mettono a punto codici di trasmissione più efficienti. Molto importanti si riveleranno le analisi di tipo matematico del problema, sviluppate a partire dagli studi dei fenomeni ondulatori del francese Joseph Fourier (1768-1830): in particolare i lavori di H. Nyquist (del 1924 la pubblicazione Alcuni fattori che influenzano la rapidità della trasmissione telegrafica), di R. Hartley (che nel 1928 pubblica la monografia dal titolo La trasmissione dell’informazione), di D. Gabor (1946, Teoria delle comunicazioni), di W. G. Tuller (1949, Limiti teorici del ritmo di trasmissione della informazione).
Una accelerazione si può ben dire drammatica a questo tipo di studi venne impressa dalla seconda guerra mondiale: i segnali da trasmettere e da garantire contro errori dovuti ai vari disturbi sono le comunicazioni al fronte e i segnali radar; bisognava fornire alle batterie contraeree dei sistemi di puntamento in grado di anticipare la posizione dell’aereo nemico per poterlo abbattere. In questo tipo di ricerche maturarono le loro idee più innovative Norberthref Wiener, padre della cibernetica e Claude Shannon.
a) Shannon definisce così il problema di cui cerca la soluzione: riprodurre in un determinato punto – in modo esatto o con una buona approssimazione – un messaggio scelto altrove. È un problema di tipo squisitamente tecnico quello che lui si pone e quando usa la parola comunicazione lo fa come sinonimo di trasmissione di segnali. Prima degli anni Quaranta questo termine non aveva l’accezione pregnante con cui noi lo usiamo oggi; era più collegato all’idea del movimento e del trasporto (vie ‘di comunicazione’ terrestri, marine, fluviali...) che non allo scambio di messaggi e, meno ancora, all’interazione simbolica. Sono proprio gli studi di Shannon (e di Norbert Wiener) – assieme alla follia della seconda guerra mondiale, rivelatrice delle tragiche conseguenze della non-comunicazione – che mettono al centro dell’attenzione del mondo scientifico questo tema. Solo dopo questi studi si è incominciato a capire la centralità di questa dimensione e se ne è progressivamente scoperta la ricchezza. È quindi profondamente ingiusto e antistorico contestare a Shannon – come capita di leggere – l’errore di ridurre a forma meccanica e lineare la comunicazione umana.
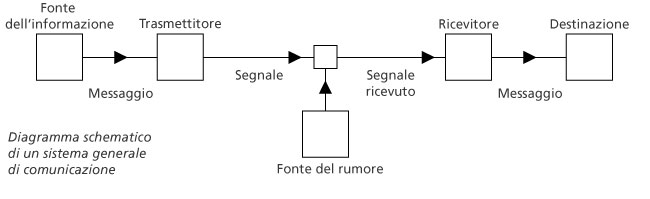
b) Già nell’introduzione della sua monografia, Shannon propone uno schema, un modello nel quale sono indicati gli elementi fondamentali che entrano in gioco in ogni trasmissione di segnali e viene indicata la relazione che li lega. Da questo momento in poi l’idea di ‘processo’ sarà stabilmente collegata con l’idea di comunicazione: ne è stato colto l’elemento caratteristico, la struttura di fondo (lo schema riprodotto nella tavola è fedele all’originale; cambia solo la lingua).
Le componenti individuate sono: la fonte (insieme dei messaggi possibili), il trasmettitore (che codifica), il canale, il ricevitore (che decodifica), il destinatario; inevitabile il rischio del rumore, della distorsione, che può cambiare – lungo il tragitto – il segnale trasmesso.
 c) Per Shannon la fonte è un insieme di messaggi possibili; di questi messaggi – per quanto riguarda la trasmissione – non viene preso in considerazione il significato. Questa affermazione sembra svuotare di importanza tutto il discorso: a che serve un sistema di trasmissione, se non ci si interessa al significato dei messaggi trasmessi?
c) Per Shannon la fonte è un insieme di messaggi possibili; di questi messaggi – per quanto riguarda la trasmissione – non viene preso in considerazione il significato. Questa affermazione sembra svuotare di importanza tutto il discorso: a che serve un sistema di trasmissione, se non ci si interessa al significato dei messaggi trasmessi?
Non è vero – come spesso si afferma – che Shannon non ritenga importante assicurare la trasmissione del significato: il significato è, infatti, ciò che vuole garantire con la massima precisione possibile. È l’analisi attenta del processo che lo porta a scoprire come non siano i significati che vengono trasmessi, ma i segnali corrispondenti. In un sistema efficiente, è deciso in partenza quali significati si vogliono trasmettere e il codice li ha collegati a dei singoli segnali.
Nel caso del telegrafo di Chappe – ad esempio – tutti gli operatori avevano la tabella delle corrispondenze; tutti gli operatori del telegrafo elettrico conoscevano l’equivalenza tra le sequenze di punti e linee e le lettere dell’alfabeto; anche due persone che parlano in italiano al telefono, prima di alzare la cornetta sanno già che determinati suoni hanno determinati significati. Ciò che non si sa – e dunque verrà fornito dal sistema – è quale figura, quale stringa di punti e linee, quale parola verrà pronunciata. L’agganciare in modo sicuro a ciascuno di questi elementi il suo significato non è un problema che interessi la trasmissione, è un dato già fissato dalle istruzioni di uso o da un dizionario.
d) Presa questa decisione, tutte le fonti con lo stesso numero di messaggi possibili, per quanto riguarda la ‘comunicazione’, sono uguali: non importa se a un interlocutore si deve indicare una parola su mille, o un libro su mille, o un bersaglio su mille: decisivo è riuscire a trasmettere al destinatario l’indicazione giusta, perché egli sa già se stiamo parlando (e dunque sceglie nel dizionario il significato indicato), se suggeriamo la lettura di un libro (in tal caso l’amico in biblioteca andrà a prendere il libro indicato) o se stiamo sparando (e dunque il collega orienta l’arma in modo opportuno). L’elemento che differenzia le fonti e rende più incerto il destinatario è la loro diversa prevedibilità: il livello di incertezza è più alto, quanto più numerosi sono i messaggi che possono provenire da quella fonte (per semplicità di ragionamento ipotizziamo che tutti i messaggi siano egualmente probabili).
e) Di qui viene la nozione di informazione come misura della complessità di una fonte o di imprevedibilità di un messaggio (va notato che le due espressioni si equivalgono: un messaggio è più prevedibile quando la fonte fornisce pochi messaggi; è invece tanto più imprevedibile quanto più numerosi ed egualmente probabili sono i messaggi della fonte).
Seguendo la proposta di R. Hurtley, Shannon adotta il codice binario, come sistema ottimale per indicare quale messaggio viene inviato da una fonte e per misurare il suo livello di imprevedibilità. Semplificando: se una fonte ha 32 messaggi possibili, è necessario e sufficiente un numero binario di cinque cifre, per indicare quale si è verificato (con 11111 indico il 32.mo, con 10001 il 17.mo; 00010 il secondo e così via); se i messaggi sono 16, bastano quattro cifre binarie; se 8, ne bastano tre; se 4, due (Bit). Se la fonte è così semplice da avere solo due messaggi possibili (di meno non si può, perché non ci sarebbe incertezza e dunque non c’è modo di comunicare nulla) basta una sola cifra binaria: 1 o 0. (Questa intuizione – che non c’è informazione se non c’è possibilità di scelta – è assai importante anche per le relazioni umane. A esempio, risulta totalmente inutile chiedere a un rivenditore se il prodotto che vende è fresco; poiché la risposta possibile è una sola, quella positiva, il richiedente non ottiene alcuna informazione utile. Generalizzando il caso, se il ricevente non lascia all’emittente la possibilità di dire la risposta giusta, non si può parlare di falsità soltanto della risposta; può essere ingiusto (e falso) anche il tipo di rapporto che la domanda cerca di instaurare. Forse il concetto di falsità come non-corrispondenza di una affermazione allo stato delle cose non basta più nell’analisi della correttezza della comunicazione umana).
Si potrebbe obiettare che il sistema decimale per fare la stessa cosa –individuare un elemento in un gruppo di trentadue– usa al massimo due cifre: 3, 17, 23... 32, mentre quello binario ne utilizza sempre cinque: 00011, 10001, 10111. È vero, ma le due cifre decimali sono scelte tra dieci, per trasmettere le quali occorrono altrettanti segnali fisici diversi; nel codice binario le cifre sono soltanto due, e dunque due soltanto sono i segnali. È molto meno esposta a errori una sequenza fatta solo da due variabili tipo 0 o 1 (tutto o niente), che non una sequenza a dieci variabili. Se ad esempio il canale di trasmissione viene disturbato (per qualche istante la tensione nel circuito subisce un innalzamento), il rumore modifica in modo analogo tutti i dati trasmessi; mentre nel caso delle cifre binarie la loro totale diversità può rimanere visibile oltre il disturbo (al posto di 0 e 1, si potrebbero trovare altre cifre, ad esempio 2 e 3: il sistema è in grado di segnalare l’errore e ne dà anche la misura, +2), per le cifre decimali – tra loro solo gradualmente diverse – questo stesso disturbo è distruttivo, dal momento che cambia una cifra in un’altra, senza che la variazione sia ‘avvertibile’: il 5 diventa 7, il 3 diventa 5, valori perfettamente accettati dal sistema.
In questo modo si è individuata una unità di misura: il bit (da binary digit, cifra binaria), che consente di usare come indice preciso della complessità di una fonte il numero di cifre binarie necessarie per identificare con sicurezza ciascuno dei suoi messaggi possibili.
Impostando così il problema, si è costruito un modello matematico del processo di tramissione e l’informazione è diventata una quantità misurabile. La sua misurazione si è rivelata importante a vari livelli: per valutare la complessità della fonte (l’entropia), per sapere la quantità di informazione caratteristica di un messaggio (il suo tasso di novità, di imprevedibilità) e anche per conoscere la capacità di un canale. Shannon approfondì in modo particolare quest’ultimo problema, riuscendo a definire dei criteri (delle formule matematiche) grazie ai quali è possibile determinare in anticipo quali messaggi si possono trasmettere in un determinato canale, anche se disturbato.
f) Importante, infine, è anche il concetto di ridondanza. Intesa in senso strettamente tecnico è il surplus di segnali adottato nella trasmissione per garantire il messaggio contro eventuali disturbi. Ad esempio ridondante è la ripetizione che spesso facciamo nel dettare il nostro numero telefonico: in questi casi il messaggio (il numero telefonico) rimane esattamente lo stesso, ciò che aumenta è il numero di segnali utilizzati affinché il ricevente trascriva il numero giusto.
I primi ad aprire la marcia sono stati i matematici impegnati nello studio della trasmissione dell’informazione (Shannon) e nella gestione dell’informazione in funzione di controllo (in particolare Wiener). Sulla loro scia si è mosso l’intero mondo scientifico. La fecondità della proposta di Shannon sta anzitutto nella astrattezza e generalizzabilità del suo modello di ‘processo di comunicazione’. Messo a punto per risolvere dei problema tecnici, si è rivelato capace di interpretare tanti altri sistemi dove vitale e continuo è lo scambio di messaggi. Si disponeva così di un nuovo punto vista e insieme di una vera e propria piattaforma teorica, che ha fatto incontrare scienze tra loro assai lontane: la linguistica, la psicologia, la psicolinguistica, la semiotica, la logica matematica, l’informatica, l’intelligenza artificiale, la microbiologia, la medicina.
Il primo è di carattere storico. Nei suoi scritti Shannon non esce dal contesto tecnico della trasmissione dei segnali; non concede spazio alla trasformazione della sua proposta a ‘metafora’ della comunicazione umana (cosa che invece fa Weaver già nelle prime righe del suo scritto). Così il titolo della pubblicazione di Shannon del 1948 è "Una teoria matematica della comunicazione"; l’anno dopo, nel volume pubblicato insieme a Weaver, esso diventa "La teoria matematica della comunicazione": è sufficiente anche una rapida lettura per accorgersi che questo cambio non è dovuto a Shannon, che ripresenta pari pari lo scritto precedente.
Il secondo errore è di merito. La comunicazione umana non può in alcun modo essere ridotta a trasmissione efficace di segnali. Anzitutto non è un processo lineare, e dunque il modello non è sufficiente; diventa indispensabile l’integrazione della ‘circolarità’ del processo proposta da Wiener con l’idea del feedback. È poi impossibile accettare – parlando di comunicazione umana – di mettere tra parentesi il significato. Shannon, che lavora con le macchine, osserva che il modo migliore per garantire efficienza e sicurezza alla trasmissione dei messaggi è considerare chiuso il sistema: le macchine infatti sono costruite per dire e fare soltanto ciò per cui sono state programmate. Nel caso dell’uomo tutto questo vale soltanto fino a quando i due interlocutori accettano di rispettare le regole (per ragioni di efficienza, infatti, l’uomo può anche accettare di comunicare come fanno le macchine). Ma non può farlo a lungo, senza rinunciare alla sua identità di sistema aperto essenzialmente interessato a ciò che è nuovo. Quando la comunicazione è umana, è sempre a rischio, perché va al di là del semplice rispetto del codice utilizzato; la sua garanzia è fornita soltanto dalla disponibilità all’interazione simbolica da parte dei soggetti coinvolti.
Un altro rilievo riguarda il valore del contesto: l’intero processo della comunicazione è di fatto legato a variabili storiche, culturali, psicologiche, ecc. Si è dovuto attendere l’avvento della pragmatica alla metà degli anni Ottanta perché il peso di queste variabili iniziare a essere pienamente riconosciuto e studiato.
Non si può dimenticare poi il ruolo determinante del ricevente (Ricezione). Chi – per analizzare la comunicazione umana – si accontenta del modello di Shannon attribuisce all’emittente un potere che di fatto non ha: non basta infatti usare correttamente i codici e disporre di un canale protetto da rumori per far arrivare il messaggio, farlo comprendere in maniera corretta e garantirne l’efficacia in termini di risultati.
Il rumore può avere valenze semantiche, non solo tecniche: non esiste solo l’interferenza sulla linea, ma anche il fatto che io sia distratto, abbia altro per la testa o sia disturbato da un terribile mal di testa. Il ricettore non è mai sotto il perfetto controllo dell’emittente.
1. Un problema antico
Il problema – la trasmissione di un messaggio a distanza – ha interessato da sempre l’umanità e a esso in ogni epoca sono state date soluzioni proporzionate alle esigenze economico-culturali, alle conoscenze teoriche e alle capacità tecnologiche disponibili. Fin dalla più remota antichità sono due le soluzioni su cui si lavora:a) affidare il messaggio a un messaggero, il quale lo recapita spostandosi fisicamente dopo averlo imparato a memoria o portandolo con sé su un qualche supporto in forma ‘scritta’ (criptato o meno);
b) utilizzare dei segnali capaci essi stessi – nonostante la distanza – di stabilire il contatto con il destinatario. È il caso dei segnali sonori (ad esempio il tam-tam, il corno, le campane...), dei segnali luminosi (il fuoco o fiaccole nella notte, i riflessi dei raggi del sole di giorno) oppure visibili da lontano (come le bandiere o il fumo...). In questo secondo caso l’uomo migliora il suo dominio sullo spazio e contrae il tempo che impiega a colmarlo, dal momento che può fare in qualche istante azioni che esigerebbero giornate, o anche mesi o anni.
La storia della comunicazione fornisce una documentazione interessante su come l’uomo abbia saputo migliorare le sue prestazioni in ambedue le direzioni, sollecitato senza tregua da una società che, crescendo e divenendo sempre più articolata, esigeva una rapidità sempre maggiore nei contatti. Più complessa infatti è l’organizzazione sociale e più vitale diviene l’interdipendenza tra attività spazialmente lontane; più alto diventa il tasso di informazione che bisogna trasmettere, più veloce deve essere lo scambio.
Seguendo il primo metodo, si è puntato a rendere sempre più veloce il messaggero (strade sempre migliori, il cavallo, il veliero, la macchina a vapore, poi i motori a combustione interna, l’aereo, i razzi...), più leggero, economico e ‘capiente’ il supporto usato (dalla pietra all’argilla, al papiro, alla pergamena, alla carta, al supporto magnetico e ottico) e più efficiente il tipo di ‘trascrizione’ (dagli ideogrammi alla scrittura sillabica, all’alfabeto fonetico completo, al linguaggio digitale...).
Nel secondo caso – quello che in questa voce ci interessa – i miglioramenti hanno puntato su un uso più efficiente del ‘contatto a distanza’ consentito dalla vista e dall’udito, giungendo a elaborare dei sistemi di segni in grado di trasmettere messaggi complessi. L’attenzione a questo secondo settore di ricerca non è nuovo. Ad esempio, lo storico greco Polibio (200-120 a. C.) nelle Storie racconta dell’invenzione di Cleonesso e di Democrito (da lui stesso ulteriormente perfezionata): con due gruppi di operatori (cinque e cinque) e dieci fiaccole, di notte o all’imbrunire, si poteva trasmettere qualsiasi messaggio. Analizzando quanto dice lo scrittore si nota che il metodo consisteva nella messa a punto di un codice secondo il quale le fiaccole – esposte o schermate e collocate in posizioni diverse – riuscivano a indicare tutte le lettere dell’alfabeto. Nonostante la sua ingegnosità, il metodo non si diffuse e finì per essere dimenticato.
Anche nel caso del telegrafo ‘ottico’ di Claude Chappe (1763-1805) – impiegato per pochi decenni, soprattutto in Francia, a partire dal 1793 – l’elemento innovativo non stava tanto nei marchingegni adottati (al posto delle fiaccole, ora, delle pale che richiamano quelle di un mulino a vento, pur se snodate e manovrabili), quanto nell’elaborazione di un codice che consente di usare in modo efficiente dei segnali riconoscibili da lontano, purché le condizioni di luce lo permettessero. Sia l’operatore che manovrava le pale sulla prima torre sia quello che sulla torre successiva interpretava le varie posizioni erano già in possesso delle tavole di corrispondenze: una certa posizione corrispondeva a una lettera dell’alfabeto, oppure – con netto miglioramento della velocità del sistema – a un intero testo già previsto dal sistema stesso, per ‘trasmettere’ il quale si indicava soltanto la corrispondente pagina del manuale di istruzioni. Non devono sfuggire la validità e il limite di questa seconda scelta: usando il telegrafo per trasmettere lettere dell’alfabeto si può trasmettere qualsiasi messaggio, ma con grande lentezza; se invece si definiscono in partenza i messaggi utili e un manuale elenca e numera i ‘pacchetti-messaggio’, si può usare il telegrafo in modo più efficiente trasmettendo soltanto i dati che individuano il ‘pacchetto’ (il numero progressivo che lo contraddistingue).
Chappe, dunque, migliora la velocità di trasmissione e la precisione (assenza di errori) del suo telegrafo ‘chiudendo’ il sistema, definendo cioè in anticipo che cosa si trasmetterà: emittente e ricevente conoscono i messaggi possibili (hanno a disposizione il prontuario), ciò che viene trasmesso è soltanto l’indicazione per individuare – tra quelli previsti – il messaggio inteso.
Le torri di Chappe – con le due grandi braccia snodate – scompaiono già nei primi decenni dell’Ottocento, non così le sue intuizioni a riguardo dell’organizzazione delle informazioni da trasmettere. Verranno riprese e approfondite ulteriormente.
La situazione cambia totalmente quando la scienza rende utilizzabili nuove forme di ‘contatto a distanza’, come l’elettricità prima e poi l’elettromagnetismo, con l’intero spettro delle onde elettromagnetiche. Si tratta di forme di energia che si muovono a velocità fantastica (nell’ordine dei 300.000 km/s) e che, pur non essendo direttamente percepibili da parte dell’uomo, diventano utilizzabili grazie alla progressiva disponibilità di strumenti che funzionano da interfaccia: il telegrafo, il telefono, la radio, la televisione, i ponti radio di ogni tipo.
Anche con questi nuovi strumenti la sfida decisiva si è giocata nella ricerca di come organizzare messaggi e segnali per ottenere la più alta efficienza. Si dice che Samuel Morse (1791-1872) – di professione pittore – abbia inventato il telegrafo e, così dicendo, si pensa al ticchettio di una manopola/interruttore manovrata da un telegrafista, a cui corrisponde, lontano a piacere, il ticchettio di un relais che appoggia una penna su una striscia di carta che scorre, in modo da tracciarvi dei punti e delle linee. Tutto questo è vero, ma il ‘nuovo’ dell’invenzione di Morse non sta in questi strumenti che egli aveva visto funzionare nelle mani di altri e che ad altri chiese di migliorare: le idee più innovative vanno riconosciute nel modo in cui egli organizzò il suo codice, in funzione di determinate caratteristiche dei messaggi da trasmettere e del canale a disposizione. Geniali e anticipatrici infatti sono alcune scelte da lui operate.
a) Suo obiettivo era trasmettere dei testi scritti. Comincia dunque con lo studio dell’alfabeto, a cui impone un ordine diverso dal tradizionale A-Z: ordina le lettere secondo il criterio della frequenza con cui esse compaiono nei testi inglesi. Non arriva ancora a servirsi di calcoli statistici per definire la probabilità di ciascuna lettera come farà C. Shannon, ma l’intuizione è già presente. Probabilmente aveva familiarità con il lavoro del tipografo, i cui cassetti non erano egualmente pieni di lettere: le ‘e’ o le ‘c’ erano molto più numerose che non lettere ‘f’ o ‘q’.
b) Sceglie i segnali da trasmettere via cavo, seguendo il criterio della sicurezza da errori: due soli segnali (chiusura del circuito per un tempo breve o per un tempo lungo), non facilmente modificabili da disturbi, tradotti all’altro capo della linea da un elettromagnete in punti (tratti brevi) e linee (tratti lunghi), tracciati su una striscia di carta in movimento, segni chiaramente riconoscibili dall’operatore.
c) Completa il codice associando le stringhe (le sequenze di punti e linee) più brevi alle lettere più frequenti: alla lettera ‘e’ associa un punto; alla ‘a’ un punto e una linea; alla ‘i’ due punti (il criterio usato è evidente, anche se non è seguito in modo perfetto; come si è detto, è utilizzato sulla base di una intuizione, non di calcoli statistici).
d) Dopo aver notato che i cavi sotterranei erano (allora) ‘inspiegabilmente’ disturbati da correnti estranee, capaci di introdurre errori non controllabili, adotta come canale le linee aeree.
Anche nel telegrafo di Morse, dunque, le vere novità non sono legate alla tecnologia utilizzata, ma al modo con cui viene trattata l’informazione: il sistema opera grazie a un codice efficiente, col quale viene sfruttata la maggiore o minore frequenza dei ‘messaggi’ da trasmettere (le lettere dell’alfabeto), utilizzando dei segnali scelti in funzione delle caratteristiche del canale per aver un miglior controllo dei possibili errori. La prova più evidente che questo è vero si ha constatando che la macchina ‘telegrafo’ ha continuato a subire modifiche e miglioramenti dall’anno della registrazione del brevetto (1837), mentre il codice Morse è rimasto ininterrottamente in uso, senza variazioni significative. (Al riguardo è interessante notare che il sistema internazionale per le chiamate di soccorso in mare ha continuato a utilizzare il codice Morse – sul canale di emergenza di 500 kHz – fino al 1° febbraio 1999, quando si è incominciato a utilizzare in forma esclusiva il GMDSS (Global Maritime Distress and Safety System), già attivo dal 1° agosto 1993. Oggi il codice Morse ha soltanto un’utilizzazione amatoriale).
Verso la fine del secolo XIX si scopre e subito si adotta un nuovo canale di comunicazione, le onde elettromagnetiche. Queste si propagano ovunque, al di là di ogni ostacolo e senza bisogno di particolari supporti. Per la loro immediata utilizzazione (Marconi) e poi per molti anni ancora si ricorre al codice Morse. Mano a mano però che si conoscono meglio i fenomeni elettrici ed elettromagnetici, vari tecnici e scienziati mettono a punto codici di trasmissione più efficienti. Molto importanti si riveleranno le analisi di tipo matematico del problema, sviluppate a partire dagli studi dei fenomeni ondulatori del francese Joseph Fourier (1768-1830): in particolare i lavori di H. Nyquist (del 1924 la pubblicazione Alcuni fattori che influenzano la rapidità della trasmissione telegrafica), di R. Hartley (che nel 1928 pubblica la monografia dal titolo La trasmissione dell’informazione), di D. Gabor (1946, Teoria delle comunicazioni), di W. G. Tuller (1949, Limiti teorici del ritmo di trasmissione della informazione).
Una accelerazione si può ben dire drammatica a questo tipo di studi venne impressa dalla seconda guerra mondiale: i segnali da trasmettere e da garantire contro errori dovuti ai vari disturbi sono le comunicazioni al fronte e i segnali radar; bisognava fornire alle batterie contraeree dei sistemi di puntamento in grado di anticipare la posizione dell’aereo nemico per poterlo abbattere. In questo tipo di ricerche maturarono le loro idee più innovative Norberthref Wiener, padre della cibernetica e Claude Shannon.
2. I lavori di Claude Elwood Shannon (1916- 2001)
Negli anni Quaranta C. E. Shannon faceva parte del gruppo di scienziati impiegati presso il centro di ricerche della compagnia Bell Telephone (USA). Proveniva dal Massachusetts Institut of Technology (MIT), dove – a 21 anni – per il master aveva elaborato una tesi risultata poi fondamentale nella progettazione dei computer (L’analisi simbolica dei circuiti a relais e commutatori). I suoi primi lavori nel Laboratorio della Bell riguardarono l’analisi matematica delle forme di de-criptazione dei messaggi (lo scopo era fornire alle forze alleate la chiave per decodificare i messaggi della marina e dell’esercito tedesco), e furono formalizzati nella monografia Communication theory of secrecy sistems (Teoria della comunicazione di sistemi di criptazione). In quelle pagine – segretate fino al 1949 – erano anticipati molti dei concetti che avrebbero poi trovato piena maturazione in una seconda monografia, A mathematical theory of communication (Una teoria matematica della comunicazione), pubblicata nel 1948 sul n. 27 del Bell System Technical Journal. La novità dell’impostazione e la fecondità della proposta attirarono subito l’attenzione del mondo scientifico. Dopo una favorevole recensione sulla rivista Scientific American, il presidente della Rockefeller Foundation, Chester Bernard, propose a un altro matematico, Warren Weaver – in quel momento a capo del dipartimento di scienze fisiche della Fondazione – di collaborare con il giovane collega per dare alle stampe un volume scritto in forma più comprensibile "into less formidable language" (in un linguaggio meno spaventoso). Nel 1949 venne pubblicato il volumetto The mathematical theory of communication (La teoria matematica della comunicazione), organizzato in due parti: nella prima Weaver introduceva la proposta di Shannon, precisandone il carattere tecnico-matematico (vi si affrontava il problema della trasmissione accurata di un segnale tra emittente e ricevente), ma insieme indicandone la grande portata teorica (la considerava infatti una teoria generale della comunicazione); nella seconda parte veniva ripubblicato il lavoro originale di Shannon.3. La t.d.i.
La teoria enunciata da Shannon – come abbiamo visto – non nacque nel vuoto, ma partiva da quanto gli studiosi precedenti avevano elaborato. Colpisce tuttavia la completezza e la precisione delle sue tesi, tant’è vero che nessuna di esse è stata smentita. I principi da lui formalizzati non solo hanno fornito un potente quadro teorico agli studi sulle telecomunicazioni, ma hanno galvanizzato un’intera generazione di studiosi, in tutti i settori della ricerca. Qui di seguito si cercherà di fornire alcuni punti della proposta di Shannon, cercando di esprimerli in modo semplificato; non ci interessa infatti la formulazione matematica della sua teoria e delle sue analisi, quanto invece la novità del suo modo di affrontare il tema della comunicazione. Per un approccio più completo e formale si troveranno in bibliografia valide indicazioni di approfondimento.a) Shannon definisce così il problema di cui cerca la soluzione: riprodurre in un determinato punto – in modo esatto o con una buona approssimazione – un messaggio scelto altrove. È un problema di tipo squisitamente tecnico quello che lui si pone e quando usa la parola comunicazione lo fa come sinonimo di trasmissione di segnali. Prima degli anni Quaranta questo termine non aveva l’accezione pregnante con cui noi lo usiamo oggi; era più collegato all’idea del movimento e del trasporto (vie ‘di comunicazione’ terrestri, marine, fluviali...) che non allo scambio di messaggi e, meno ancora, all’interazione simbolica. Sono proprio gli studi di Shannon (e di Norbert Wiener) – assieme alla follia della seconda guerra mondiale, rivelatrice delle tragiche conseguenze della non-comunicazione – che mettono al centro dell’attenzione del mondo scientifico questo tema. Solo dopo questi studi si è incominciato a capire la centralità di questa dimensione e se ne è progressivamente scoperta la ricchezza. È quindi profondamente ingiusto e antistorico contestare a Shannon – come capita di leggere – l’errore di ridurre a forma meccanica e lineare la comunicazione umana.
b) Già nell’introduzione della sua monografia, Shannon propone uno schema, un modello nel quale sono indicati gli elementi fondamentali che entrano in gioco in ogni trasmissione di segnali e viene indicata la relazione che li lega. Da questo momento in poi l’idea di ‘processo’ sarà stabilmente collegata con l’idea di comunicazione: ne è stato colto l’elemento caratteristico, la struttura di fondo (lo schema riprodotto nella tavola è fedele all’originale; cambia solo la lingua).
Le componenti individuate sono: la fonte (insieme dei messaggi possibili), il trasmettitore (che codifica), il canale, il ricevitore (che decodifica), il destinatario; inevitabile il rischio del rumore, della distorsione, che può cambiare – lungo il tragitto – il segnale trasmesso.
Tavola 1

Non è vero – come spesso si afferma – che Shannon non ritenga importante assicurare la trasmissione del significato: il significato è, infatti, ciò che vuole garantire con la massima precisione possibile. È l’analisi attenta del processo che lo porta a scoprire come non siano i significati che vengono trasmessi, ma i segnali corrispondenti. In un sistema efficiente, è deciso in partenza quali significati si vogliono trasmettere e il codice li ha collegati a dei singoli segnali.
Nel caso del telegrafo di Chappe – ad esempio – tutti gli operatori avevano la tabella delle corrispondenze; tutti gli operatori del telegrafo elettrico conoscevano l’equivalenza tra le sequenze di punti e linee e le lettere dell’alfabeto; anche due persone che parlano in italiano al telefono, prima di alzare la cornetta sanno già che determinati suoni hanno determinati significati. Ciò che non si sa – e dunque verrà fornito dal sistema – è quale figura, quale stringa di punti e linee, quale parola verrà pronunciata. L’agganciare in modo sicuro a ciascuno di questi elementi il suo significato non è un problema che interessi la trasmissione, è un dato già fissato dalle istruzioni di uso o da un dizionario.
d) Presa questa decisione, tutte le fonti con lo stesso numero di messaggi possibili, per quanto riguarda la ‘comunicazione’, sono uguali: non importa se a un interlocutore si deve indicare una parola su mille, o un libro su mille, o un bersaglio su mille: decisivo è riuscire a trasmettere al destinatario l’indicazione giusta, perché egli sa già se stiamo parlando (e dunque sceglie nel dizionario il significato indicato), se suggeriamo la lettura di un libro (in tal caso l’amico in biblioteca andrà a prendere il libro indicato) o se stiamo sparando (e dunque il collega orienta l’arma in modo opportuno). L’elemento che differenzia le fonti e rende più incerto il destinatario è la loro diversa prevedibilità: il livello di incertezza è più alto, quanto più numerosi sono i messaggi che possono provenire da quella fonte (per semplicità di ragionamento ipotizziamo che tutti i messaggi siano egualmente probabili).
e) Di qui viene la nozione di informazione come misura della complessità di una fonte o di imprevedibilità di un messaggio (va notato che le due espressioni si equivalgono: un messaggio è più prevedibile quando la fonte fornisce pochi messaggi; è invece tanto più imprevedibile quanto più numerosi ed egualmente probabili sono i messaggi della fonte).
Seguendo la proposta di R. Hurtley, Shannon adotta il codice binario, come sistema ottimale per indicare quale messaggio viene inviato da una fonte e per misurare il suo livello di imprevedibilità. Semplificando: se una fonte ha 32 messaggi possibili, è necessario e sufficiente un numero binario di cinque cifre, per indicare quale si è verificato (con 11111 indico il 32.mo, con 10001 il 17.mo; 00010 il secondo e così via); se i messaggi sono 16, bastano quattro cifre binarie; se 8, ne bastano tre; se 4, due (Bit). Se la fonte è così semplice da avere solo due messaggi possibili (di meno non si può, perché non ci sarebbe incertezza e dunque non c’è modo di comunicare nulla) basta una sola cifra binaria: 1 o 0. (Questa intuizione – che non c’è informazione se non c’è possibilità di scelta – è assai importante anche per le relazioni umane. A esempio, risulta totalmente inutile chiedere a un rivenditore se il prodotto che vende è fresco; poiché la risposta possibile è una sola, quella positiva, il richiedente non ottiene alcuna informazione utile. Generalizzando il caso, se il ricevente non lascia all’emittente la possibilità di dire la risposta giusta, non si può parlare di falsità soltanto della risposta; può essere ingiusto (e falso) anche il tipo di rapporto che la domanda cerca di instaurare. Forse il concetto di falsità come non-corrispondenza di una affermazione allo stato delle cose non basta più nell’analisi della correttezza della comunicazione umana).
Si potrebbe obiettare che il sistema decimale per fare la stessa cosa –individuare un elemento in un gruppo di trentadue– usa al massimo due cifre: 3, 17, 23... 32, mentre quello binario ne utilizza sempre cinque: 00011, 10001, 10111. È vero, ma le due cifre decimali sono scelte tra dieci, per trasmettere le quali occorrono altrettanti segnali fisici diversi; nel codice binario le cifre sono soltanto due, e dunque due soltanto sono i segnali. È molto meno esposta a errori una sequenza fatta solo da due variabili tipo 0 o 1 (tutto o niente), che non una sequenza a dieci variabili. Se ad esempio il canale di trasmissione viene disturbato (per qualche istante la tensione nel circuito subisce un innalzamento), il rumore modifica in modo analogo tutti i dati trasmessi; mentre nel caso delle cifre binarie la loro totale diversità può rimanere visibile oltre il disturbo (al posto di 0 e 1, si potrebbero trovare altre cifre, ad esempio 2 e 3: il sistema è in grado di segnalare l’errore e ne dà anche la misura, +2), per le cifre decimali – tra loro solo gradualmente diverse – questo stesso disturbo è distruttivo, dal momento che cambia una cifra in un’altra, senza che la variazione sia ‘avvertibile’: il 5 diventa 7, il 3 diventa 5, valori perfettamente accettati dal sistema.
In questo modo si è individuata una unità di misura: il bit (da binary digit, cifra binaria), che consente di usare come indice preciso della complessità di una fonte il numero di cifre binarie necessarie per identificare con sicurezza ciascuno dei suoi messaggi possibili.
Impostando così il problema, si è costruito un modello matematico del processo di tramissione e l’informazione è diventata una quantità misurabile. La sua misurazione si è rivelata importante a vari livelli: per valutare la complessità della fonte (l’entropia), per sapere la quantità di informazione caratteristica di un messaggio (il suo tasso di novità, di imprevedibilità) e anche per conoscere la capacità di un canale. Shannon approfondì in modo particolare quest’ultimo problema, riuscendo a definire dei criteri (delle formule matematiche) grazie ai quali è possibile determinare in anticipo quali messaggi si possono trasmettere in un determinato canale, anche se disturbato.
f) Importante, infine, è anche il concetto di ridondanza. Intesa in senso strettamente tecnico è il surplus di segnali adottato nella trasmissione per garantire il messaggio contro eventuali disturbi. Ad esempio ridondante è la ripetizione che spesso facciamo nel dettare il nostro numero telefonico: in questi casi il messaggio (il numero telefonico) rimane esattamente lo stesso, ciò che aumenta è il numero di segnali utilizzati affinché il ricevente trascriva il numero giusto.
4. La fecondità della t.d.i.
Gli anni Quaranta sono stati un decennio di atroci contraddizioni ma anche di grandi speranze: si è chiusa una stagione di orrori inimmaginabili per commettere i quali ogni risorsa tecnica e scientifica è stata usata allo scopo di annientare con maggiore efficienza l’uomo; in totale contrasto, negli stessi anni, si è avviato lo sviluppo di un nuovo modo di considerare la realtà, non più soltanto in termini di materia e di energia, ma anche in termini di scambio di segnali, di sistemi ad autocontrollo, di macchine intelligenti, tanto da nutrire l’utopia di una società razionale e senza barriere.I primi ad aprire la marcia sono stati i matematici impegnati nello studio della trasmissione dell’informazione (Shannon) e nella gestione dell’informazione in funzione di controllo (in particolare Wiener). Sulla loro scia si è mosso l’intero mondo scientifico. La fecondità della proposta di Shannon sta anzitutto nella astrattezza e generalizzabilità del suo modello di ‘processo di comunicazione’. Messo a punto per risolvere dei problema tecnici, si è rivelato capace di interpretare tanti altri sistemi dove vitale e continuo è lo scambio di messaggi. Si disponeva così di un nuovo punto vista e insieme di una vera e propria piattaforma teorica, che ha fatto incontrare scienze tra loro assai lontane: la linguistica, la psicologia, la psicolinguistica, la semiotica, la logica matematica, l’informatica, l’intelligenza artificiale, la microbiologia, la medicina.
5. T.d.i. e comprensione della comunicazione umana: bilancio critico
Negli anni Cinquanta, come anche nei successivi, molto spesso il modello di Shannon è stato applicato ‘in modo diretto’ alla comunicazione umana, seguendo una tendenza già evidente nella ‘traduzione’ che Weaver aveva fatto nel 1949 della proposta teorica del collega. In questo modo però si sono commessi due errori.Il primo è di carattere storico. Nei suoi scritti Shannon non esce dal contesto tecnico della trasmissione dei segnali; non concede spazio alla trasformazione della sua proposta a ‘metafora’ della comunicazione umana (cosa che invece fa Weaver già nelle prime righe del suo scritto). Così il titolo della pubblicazione di Shannon del 1948 è "Una teoria matematica della comunicazione"; l’anno dopo, nel volume pubblicato insieme a Weaver, esso diventa "La teoria matematica della comunicazione": è sufficiente anche una rapida lettura per accorgersi che questo cambio non è dovuto a Shannon, che ripresenta pari pari lo scritto precedente.
Il secondo errore è di merito. La comunicazione umana non può in alcun modo essere ridotta a trasmissione efficace di segnali. Anzitutto non è un processo lineare, e dunque il modello non è sufficiente; diventa indispensabile l’integrazione della ‘circolarità’ del processo proposta da Wiener con l’idea del feedback. È poi impossibile accettare – parlando di comunicazione umana – di mettere tra parentesi il significato. Shannon, che lavora con le macchine, osserva che il modo migliore per garantire efficienza e sicurezza alla trasmissione dei messaggi è considerare chiuso il sistema: le macchine infatti sono costruite per dire e fare soltanto ciò per cui sono state programmate. Nel caso dell’uomo tutto questo vale soltanto fino a quando i due interlocutori accettano di rispettare le regole (per ragioni di efficienza, infatti, l’uomo può anche accettare di comunicare come fanno le macchine). Ma non può farlo a lungo, senza rinunciare alla sua identità di sistema aperto essenzialmente interessato a ciò che è nuovo. Quando la comunicazione è umana, è sempre a rischio, perché va al di là del semplice rispetto del codice utilizzato; la sua garanzia è fornita soltanto dalla disponibilità all’interazione simbolica da parte dei soggetti coinvolti.
Un altro rilievo riguarda il valore del contesto: l’intero processo della comunicazione è di fatto legato a variabili storiche, culturali, psicologiche, ecc. Si è dovuto attendere l’avvento della pragmatica alla metà degli anni Ottanta perché il peso di queste variabili iniziare a essere pienamente riconosciuto e studiato.
Non si può dimenticare poi il ruolo determinante del ricevente (Ricezione). Chi – per analizzare la comunicazione umana – si accontenta del modello di Shannon attribuisce all’emittente un potere che di fatto non ha: non basta infatti usare correttamente i codici e disporre di un canale protetto da rumori per far arrivare il messaggio, farlo comprendere in maniera corretta e garantirne l’efficacia in termini di risultati.
Il rumore può avere valenze semantiche, non solo tecniche: non esiste solo l’interferenza sulla linea, ma anche il fatto che io sia distratto, abbia altro per la testa o sia disturbato da un terribile mal di testa. Il ricettore non è mai sotto il perfetto controllo dell’emittente.
Video
Non ci sono video per questa voce
Bibliografia
- ANGELERI Emanuele, Informazione. Significato e universalità, UTET, Torino 2000.
- BAR-HILLEL J., Analisi della teoria dell'informazione in ROSSI P. A. (ed.), Cibernetica e teoria dell'informazione, La Scuola, Brescia 1978.
- CAREY James W., Technology and ideology. The case of the telegraph in Id., Communication as culture. Essays in media and society, Unwin Hyman, Boston (MA) 1988.
- CIOTTI Fabio - RONCAGLIA Gino, Il mondo digitale. Introduzione ai nuovi media, Laterza, Roma 2003.
- ESCARPIT Robert, Teoria dell’informazione e della comunicazione, Ed. Riuniti, Roma 1979.
- KRIPPENDORFF Klaus, Information theory. Structural models for qualitative data, Sage, London 1986.
- MILES Ian - RUSH Howard - TURNER Kevin - BESSANT John, I.T. Information Technology, Baskerville, Bologna 1993.
- PIERCE John R., La teoria dell’informazione. Simboli, codici, messaggi, Mondadori, Milano 1971.
- ROGER Jacques, Teoria dell’informazione, Il Mulino, Bologna 1974.
- ROSSI Paolo Aldo (ed.), Cibernetica e teoria dell’informazione, La Scuola, Brescia 1978.
- SHANNON Claude E. - WEAVER Warren, La teoria matematica della comunicazione, Etas Libri, Milano 1983, Ediz. originale disponibile in rete: http://www.magmamater.cl/MatheComm.pdf.
- SLOAN Neil - WYNER Aaron D. (eds.), Claude Elwood Shannon. Collected papers, IEEE Press, New York 1993.
- WIENER Norbert, The human use of human beings. Cybernetics and society, Free Association Books, London 1989, In rete: http://21stcenturywiener.org/wp-content/uploads/2013/11/The-Human-Use-of-Human-Beings-by-N.-Wiener.pdf.
- WIENER Norbert, Introduzione alla cibernetica. L'uso umano degli esseri umani, Boringhieri, Torino 1976.
- WIENER Norbert, La cibernetica. Controllo e comunicazione nell'animale e nella macchina, Il Saggiatore, Milano 1968.
Documenti
Non ci sono documenti per questa voce
Links
Note
Come citare questa voce
Lever Franco , Teoria dell'informazione, in Franco LEVER - Pier Cesare RIVOLTELLA - Adriano ZANACCHI (edd.), La comunicazione. Dizionario di scienze e tecniche, www.lacomunicazione.it (31/07/2025).
 Il testo è disponibile secondo la licenza CC-BY-NC-SA
Il testo è disponibile secondo la licenza CC-BY-NC-SACreative Commons Attribuzione-Non commerciale-Condividi allo stesso modo
1263





